On-Axis Chromatic Image Point Formation
For A Double Gauss Lens
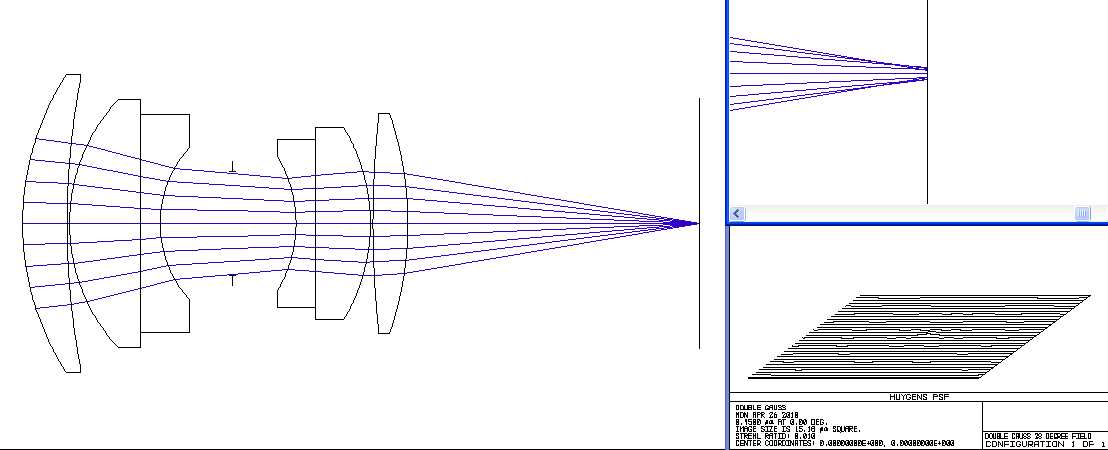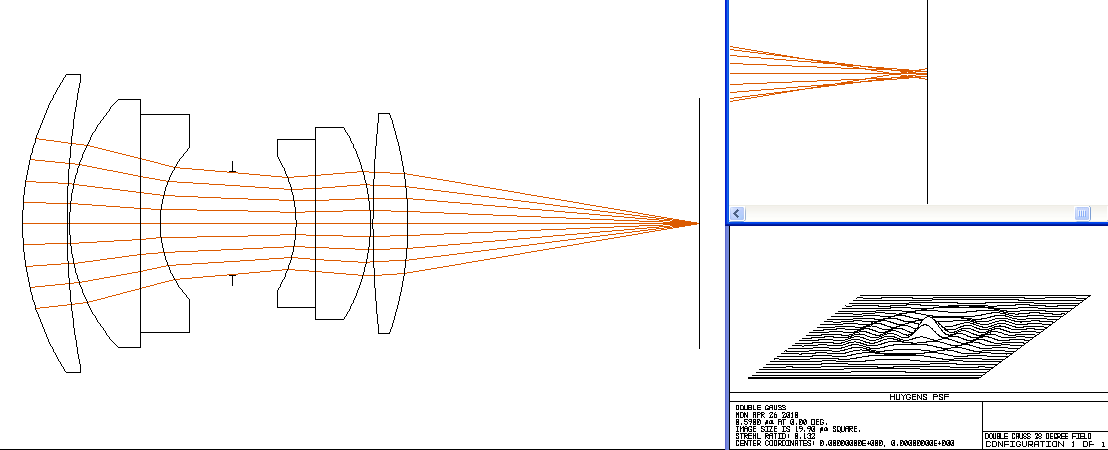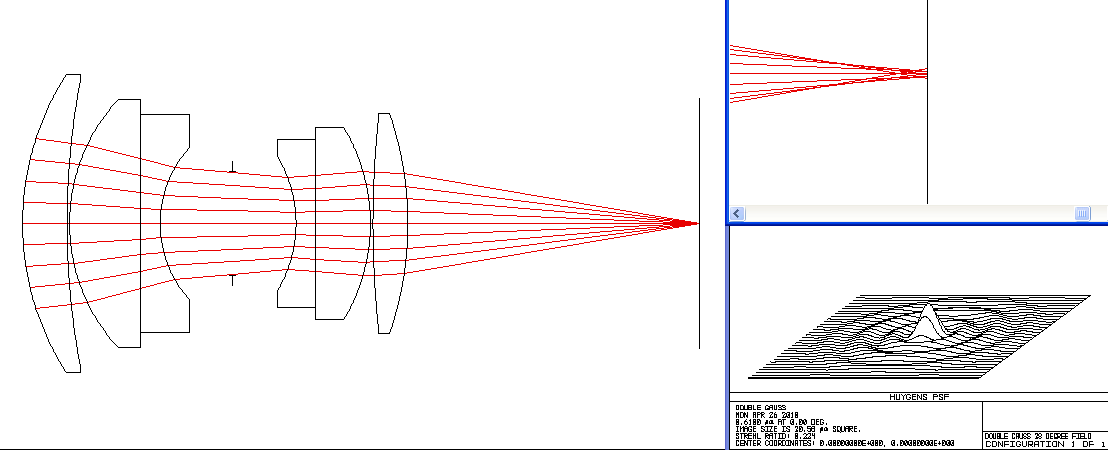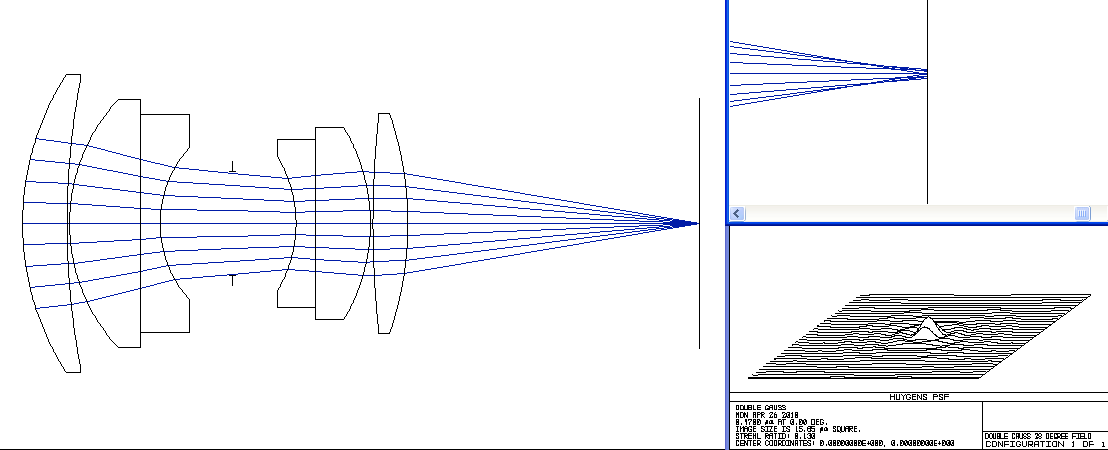 |
Double Gauss Photographic Lens
f/3.0, On Axis, Wavelengths = 0.450 to 0.670 microns (blue to red)
Second, notice that at some wavelengths more light is concentrated in the central peak than at other wavelengths. That energy is drawn from the circular rings. Even still, the best this lens does with the image plane at the chosen location is still about 4 times lower than perfection. Also consider that when the central peak is minimized, the rings get more power and the effect is a chromatic blurring of a point image. This mechanism is the origin of the famous "purple fringing" effect.
But aha you say. Just change the position of the image plane and you'll find a position where the rays better come to a point. That's true--for this image point. But you have to consider all the other image points across the sensor (remember all that money you paid for all those megapixels?) The lens designer has chosen the image plane position so that the best focus is obtained for all points in the image using some sort of best average, or equivalently least worst, algorithm.
OK you say, but you can also remove the upper and lower rays forming the image point by stopping down the lens to a higher f/no. Yes, that's true--up to a point. Because while you're removing the rays that cause the lateral chromatic error, a smaller f/no means the central peak gets wider, blurring your image. This process of spreading out the width of the central imae peak is due to the wave phenomenon called diffraction.
And incidentally, the diameter of that perfect peak is given by the formula above. It will contain about 84 percent of the light making up the energy that enter the lens for that image position. Optical perfection is nearly impossible to attain in practical photographic lens. Approaching it usually requires a source of government funding.