Image Point Formation
For A Double Gauss Lens




Double Gauss Photographic Lens
f/3.0, Object Field of View = 28 degrees, Wavelength = 0.5876 microns (green)

The lens shown in this animation is an old, old formulation--a double Gauss lens operating at f/3. Modern lenses start with this basic design and considerably improve performance with the addition of more lens groups (to minimize geometric aberrations) and more interesting categories of glasses (to control chromatic aberrations.) For example, see this lens. But no matter their configuration, all lens should form point images that are well-defined if they're to be considered "sharp." That "well-defined point" is not a perfect point, but a spread of light, exactly structured with a bright central lobe and dimmer surrounding rings. That structure is called the Airy disk and is discussed everywhere, like here. You can get a slight hint of this structure for the point in the center of the image plane for this double Gauss lens example.

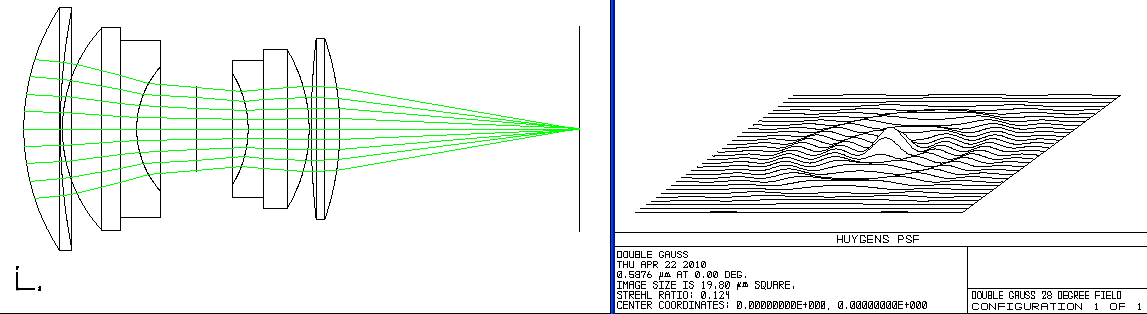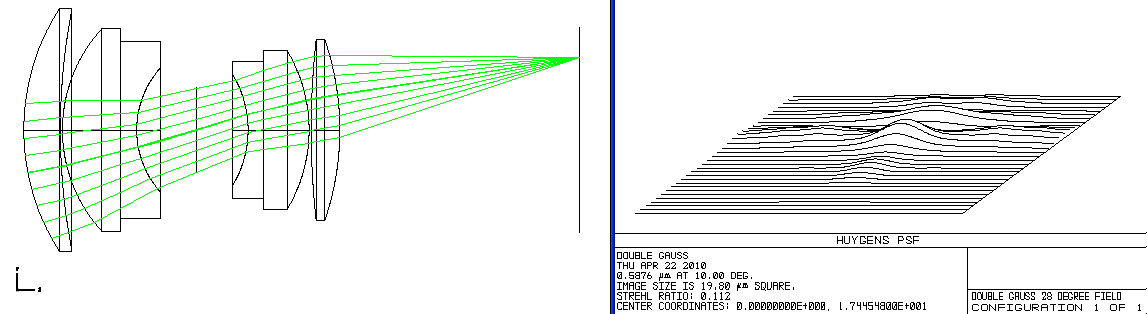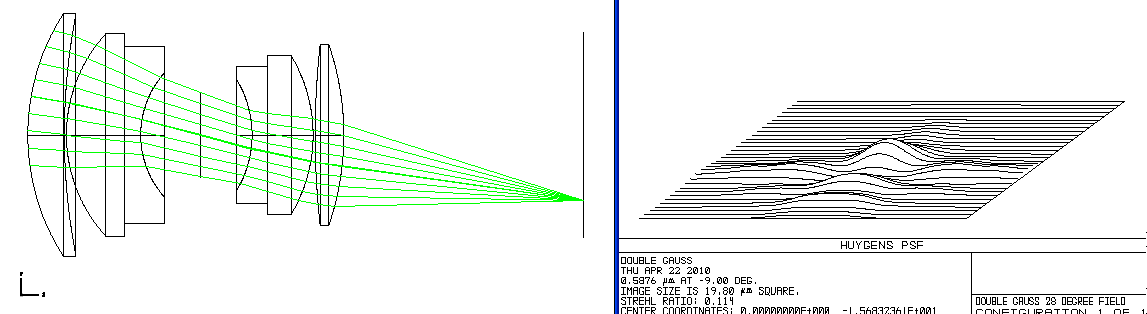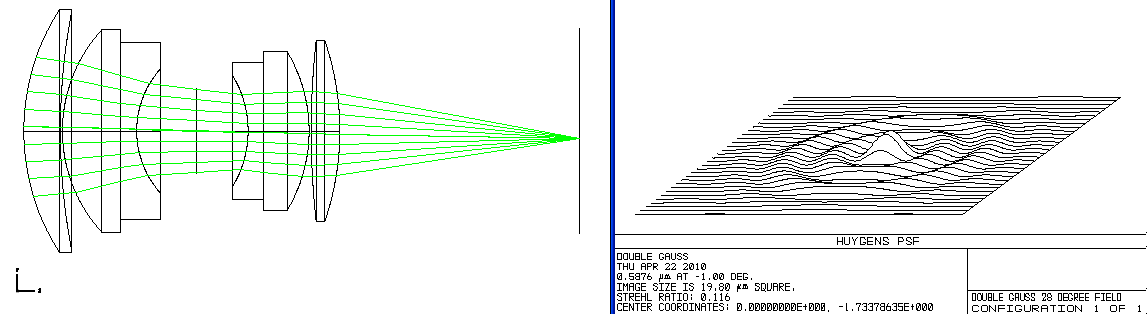
There are 27 objects in this simulation that are very far to the left of the lens. They are positioned on a straight line at infinity from minus fourteen degrees to plus fourteen degrees in one degree increments. We'd like this optic to form 27 perfect point images to the right of the lens in a straight line on the flat plane of our sensor.

I've selected 9 rays from from each object and traced them through the lens so you can see how they bend and attempt to focus at the image plane. The right half panel displays close-ups of those 27 imaged points, cropped by rectangles 19.8 microns on a side. (A micron is 1/1000th of a millimeter.) This rectangle does not represent the image sensor which is about 49.2 mm in size (or 49,200 microns.) What we'd like to see is the Airy disk for each image point which stays located at the same position, not wandering around inside the rectangle. A perfect image point would have a central lobe of energy about 8 times higher than what you see for the image at 0 degrees with a diameter of only 2.135 microns. That is clearly not happening for our double Gauss lens. The further you get away from the center of the image, the distinct, central peak collapses and spreads out into a spread of lumps. This is why you can conclude this lens is not very sharp.

And even this display is only part of the story. The image points here are for only one color or wavelength. Each separate wavelength from blue to red has its own distinct sets of points--some much worse than this.


Double Gauss Lens Performance
Using Encircled Energy Metric



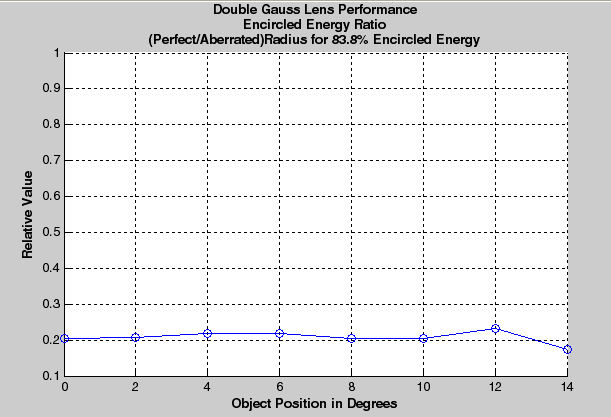f/3.0, Object Field of View = 28 Degrees, Wavelengths: Polychromatic

Using our encircled energy metric, you can see that this lens performs rather poorly spreading out the light for each point over an area 25 times larger than we'd like. About the best you can say is this lens is uniformly poor across the entire image field. It would be great to see any lens performing with values between 0.8 and 1.0. Be prepared to pay for this performance.

And a final note. The data in this chart is derived from a mathematical analysis of an optimized design that resides in the computer. In practice, you can expect any lens performance to be worse than this because of inevitable manufacturing errors like imprecisely made surface curvatures, and lens decentration errors both axial and tangential.
Return To Dennis' Lens Blog
Return To Dennis' Home Page

All Pictures and Movies on this Website Page are copyrighted by Dennis Hancock
©2010 Dennis Hancock